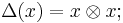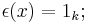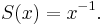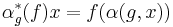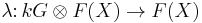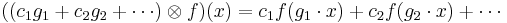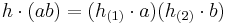Group Hopf algebra

In mathematics, the group Hopf algebra of a given group is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.

1 Definition
2 Hopf algebra structure
3 Symmetries of group actions
4 Hopf module algebras and the Hopf smash product
5 References

Definition

Let G be an arbitrary group and k a field. The group Hopf algebra of G over k, denoted kG (or k[G]), is as a set (and vector space) the free vector space on G over k. As an algebra, its product is defined by linear extension of the group composition in G, with multiplicative unit the identity in G; this product is also known as convolution.

Note that while the group algebra of a finite group can be identified with the space of functions on the group, for an infinite group these are different. The group algebra, consisting of finite sums, corresponds to functions on the group that vanish for cofinitely many points; topologically (using the discrete topology), these correspond to functions with compact support.

However, the group algebra k[G] and the space of function k^G := Hom(G,k) are dual: given an element of the group algebra 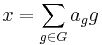$x = \sum_{g\in G} a_g g$ and a function on the group 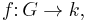$f\colon G \to k,$ these pair to give an element of k via 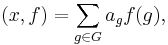$(x,f) = \sum_{g\in G} a_g f(g),$ which is a well-defined sum because it is finite.

Hopf algebra structure

We give kG the structure of a cocommutative Hopf algebra by defining the coproduct, counit, and antipode to be the linear extensions of the following maps defined on G:

$\Delta(x) = x \otimes x;$

$\epsilon(x) = 1_{k};$

$S(x) = x^{-1}.$

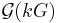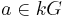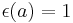The required Hopf algebra compatibility axioms are easily checked. Notice that $\mathcal{G}(kG)$ , the set of group-like elements of kG (i.e. elements $a \in kG$ such that $\Delta(a) = a \otimes a$ and $\epsilon(a)=1$ ), is precisely G.

Symmetries of group actions

Let G be a group and X a topological space. Any action 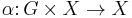$\alpha\colon G \times X \to X$ of G on X gives a homomorphism 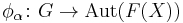$\phi_\alpha\colon G \to \mathrm{Aut}(F(X))$ , where F(X) is an appropriate algebra of k-valued functions, such as the Gelfand-Naimark algebra 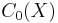$C_0(X)$ of continuous functions vanishing at infinity. 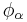$\phi_{\alpha}$ is defined by 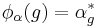$\phi_\alpha(g)= \alpha^*_g$ with the adjoint 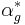$\alpha^*_{g}$ defined by

$\alpha^*_g(f)x = f(\alpha(g,x))$

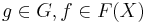for $g \in G, f \in F(X)$ , and $x \in X$ .

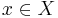This may be described by a linear mapping

$\lambda\colon kG \otimes F(X) \to F(X)$

$((c_1 g_1 %2B c_2 g_2 %2B \cdots ) \otimes f)(x) = c_1 f(g_1 \cdot x) %2B c_2 f(g_2 \cdot x) %2B \cdots$

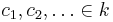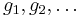where $c_1,c_2,\ldots \in k$ , $g_1, g_2,\ldots$ are the elements of G, and 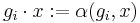$g_i \cdot x�:= \alpha(g_i,x)$ , which has the property that group-like elements in kG give rise to automorphisms of F(X).

$\lambda$ endows F(X) with an important extra structure, described below.

Hopf module algebras and the Hopf smash product

Let H be a Hopf algebra. A (left) Hopf H-module algebra A is an algebra which is a (left) module over the algebra H such that 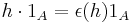$h \cdot 1_A = \epsilon(h)1_A$ and

$h \cdot (ab) = (h_{(1)} \cdot a)(h_{(2)} \cdot b)$

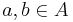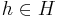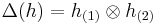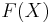whenever $a,b \in A$ , $h \in H$ and $\Delta(h) = h_{(1)} \otimes h_{(2)}$ in sumless Sweedler notation. Obviously, $\lambda$ as defined in the previous section turns $F(X)$ into a left Hopf kG-module algebra, and hence allows us to consider the following construction.

Let H be a Hopf algebra and A a left Hopf H-module algebra. The smash product algebra 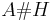$A \# H$ is the vector space 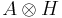$A \otimes H$ with the product

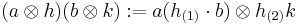$(a \otimes h)(b \otimes k)�:= a(h_{(1)} \cdot b) \otimes h_{(2)}k$ ,

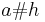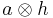and we write $a \# h$ for $a \otimes h$ in this context.

In our case, A = F(X) and H = kG, and we have

$(a \# g_1)(b \# g_2) = a(g_1 \cdot b) \# g_1 g_2$ .

In this case the smash product algebra 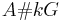$A \# kG$ is also denoted by $A \# G$ .

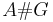The cyclic homology of Hopf smash products has been computed.^[1] However, there the smash product is called a crossed product and denoted 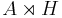$A \rtimes H$ - not to be confused with the crossed product derived from 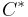$C^{*}$ -dynamical systems.^[2]

References

^ R. Akbarpour and M. Khalkhali (2003) Hopf Algebra Equivariant Cyclic Homology and Cyclic Homology of Crossed Product Algebras. arXiv:math/0011248v6 [math.KT]. J. reine angew. Math. 559 137–152.
^ Gracia-Bondia, J. et al. Elements of Noncommutative Geometry. Birkauser: Boston, 2001. ISBN 0-8176-4124-6